No se trata de jugar por jugar, se trata de aprender jugando.
La palabra juego procede del latín jŏcus ¨broma¨,¨chanza¨, ¨diversión¨. El juego y la cultura van estrechamente unidos y su papel ha sido señalado repetidamente. Muchos psicólogos y antropólogos han dedicado estudios e investigaciones al juego. Schiller(1928:12) con su famosa frase "el hombre no está completo sino cuandojuega" nos llama la atención sobre el juego
Veamos también que el término «escuela» proviene del griego clásico σχολή (skholḗ) por mediación del sclatín hola. Curiosamente el significado original en griego era de 'ocio, tranquilidad, tiempo libre', que luego derivó a aquello que se hace durante el tiempo libre y, más concretamente, aquello que merece la pena hacerse, de donde acabó significando 'estudio' (por oposición a los juegos). En el perído helenístico pasó a designar a las escuelas filosóficas, y de ahí, por extensión, tomó el significado actual de «centro de estudios». (Wilkipedia)
Si pensamos en el juego en la escuela podemos decir que es un recurso para el trabajo con los alumnos. Se emplea mucho en el nivel inicial, algo en el nivel primario y casi nada en los otros niveles, salvo temas específicos. El porque de esto radica en considerar al juego como “para niños” o una pérdida de tiempo ya que deben enseñarse temas en particular. Muchas veces se lo emplea como “relleno” de clases cuando no se sabe que hacer, cuando los alumnos están “aburridos” y, por supuesto, se cae en la improvisación. Entendemos que para que esto no suceda y sea un buen recurso de enseñanza el docente debe reflexionar y analizar dónde, cuándo, cómo y qué tipo de juegos debe presentar en el aula.
Son importantes recursos ya que pueden convertir al proceso de enseñanza aprendizaje en un momento más agradable y participativo, esto no significa que el incluir un juego en una clase asegure el aprendizaje de un tema. Deben estar de acuerdo con la práctica pedagógica del docente y tener en cuenta objetivos acordes a los contenidos que se quieren transmitir.
La presentación de conceptos matemáticos está ligada a la idea de juego. En la actualidad podemos ver gran cantidad de ellos en páginas web, juegos para computadora y programas televisivos. Por supuesto no todo sirve, no todo permite enseñar aquello que queremos que los chicos aprendan.
El juego que tiene bien definidas sus reglas y que posee cierta riqueza de movimientos, suele prestarse muy frecuentemente a un tipo de análisis intelectual cuyas características son muy semejantes a las que presenta el desarrollo matemático
A lo largo de la historia se han presentado distintas situaciones lúdicas que han llevado al descubrimiento de interesantes herramientas matemáticas. Por ejemplo: En 1735, Euler (1707-1783), oyó hablar del problema de los siete puentes de Königsberg, sobre la posibilidad de organizar un paseo que cruzase todos y cada uno de los puentes una sola vez. Su solución constituyó el comienzo de una nueva rama de la matemática, la teoría de grafos y con ella de la topología general. Los biógrafos de Gauss (1777-1855) cuentan que el Princeps Mathematicorum era un gran aficionado a jugar a las cartas y que cada día anotaba cuidadosamente las manos que recibía para analizarlas después estadísticamente.
Según cuenta Martin Gardner, Albert Einstein (1879-1955), tenía toda una estantería de su biblioteca particular dedicada a libros sobre juegos matemáticos. Así podríamos seguir nombrando matemáticos que veían en los juegos una fuente de investigación para el desarrollo de nuevos conceptos.
Los juegos pueden ser utilizados en distintos momentos de la clase: para introducir un asunto, para fijar y practicar los contenidos después de una explicación o para hacer una revisión, incluso puede ser el punto central de la misma.
Para que este sea un recurso válido de enseñanza se debe tener en claro, qué se quiere enseñar, cuáles son los objetivos que se proponen, y a quien va dirigido, recordar que no funcionan solos, requieren del docente, antes, durante y después.
La matemática es, en gran parte, juego, y el juego puede, en muchas ocasiones, analizarse mediante instrumento matemáticos. En general las reglas del juego no necesitan de grandes y complicadas introducciones. Los juegos buscan diversión y un accionar inmediato. Muchas situaciones matemáticas también permiten esto, sencillez e inmediatez, pero la matemática va más allá experimenta desde la realidad para poder generar instrumentos que permitan solucionar nuevos problemas.
La tarea de comprender y generalizar conceptos matemáticos no es una tarea sencilla para los alumnos de los distintos niveles, el empleo de juegos permite impregnar de un sabor más estimulante e incluso más atractiva la tarea
Las modificaciones que se hacen en los juegos, ya sea en sus reglas u otros aspectos del mismo, deben permitir evolucionar en los conceptos a enseñar con ellos.
Juegos de desplazamientos.
Los desplazamientos de un móvil pueden ser presentados sobre una serie de casilleros o bien sobre tableros con indicaciones mediante referencias extrínsecas. Por ejemplo: los lados de los tableros de un juego pueden estar indicados con distintos colores de tal manera que se indicará “hacia el color azul”, “hacia el color rojo”, etc. O referencias intrínsecas avanzar tantos casilleros a la derecha avanzar sobre bifurcaciones o sobre un plano de calles de una ciudad. Avanzar o retroceder casillero a casillero, saltar hasta un casillero de un color determinado o hasta un número determinado, o saltar tantos casilleros como indica el dado, etc. Proponer juegos con distintas modificaciones o variantes podrá permitir enseñar un mismo concepto bajo apariencias diferentes enriqueciéndolo.
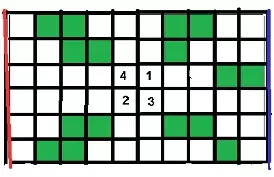
Caminando
Material: tablero que figura arriba. Fichas de cuatro colores diferentes. Dado numerado solo con 1 y 2.
Cantidad de jugadores: cuatro por equipo.
Desarrollo: inicialmente las fichas están ubicadas en los casilleros del centro (numeradas del 1 al 4), se tira el dado, por turno, y se deben ir los jugadores 1 y 3 hacia el azul, y 2 y 4 hacia el rojo. Pueden hacerlo buscando el camino más corto o más largo de acuerdo a lo que se desee trabajar.
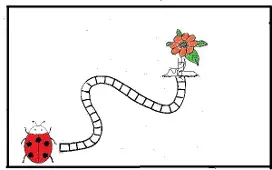
Llegando a la flor.
Material: tablero con casilleros en blanco.
Un dado., fichas
Desarrollo: tirar el dado y avanzar tantos casilleros como indica el dado.
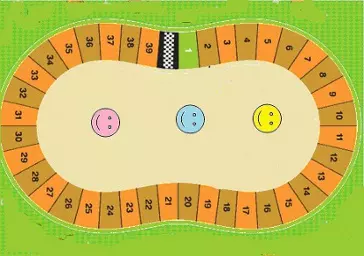
Carrera feliz
Modificación: los casilleros tienen números marcados, 1,2 3, etc.
Se tira el dado y se va avanzando de acuerdo a lo que sale en el dado.
Se puede observar que algunos niños al tirar el dado la primera vez, por ejemplo sale 4, colocan la ficha en el número 4. Al tirar el dado por segunda vez (sale 3), toman la ficha y la colocan en el 3, no advirtiendo que deben contar a partir del 4, lugar donde está su ficha. El tablero numerado genera la necesidad de aprender algo nuevo, ir contando a partir de la ubicación de su ficha.
Algunos juegos para aprender los números.
Sigue el tres (basado en un juego de cartas del Japón). Sala de 4 años.
Materiales: 30 cartas numeradas del 1 al 5 de seis diseños diferentes.
Cantidad de jugadores: para 4 o 5 niños
Desarrollo: se reparten todas las cartas entre los jugadores. Por turno, cada uno descarta sobre la mesa todos los números 3 que tenga, acomodándolos boca arriba, hasta que queden alineados todos los diseños.
La rueda continúa debiendo completar la serie (ascendente o descendente) a partir del 3, respetando siempre el orden (no se puede “saltear”) y el diseño. Si no posee la carta adecuada, pierde un turno. Gana el jugador que termina antes con todas sus cartas.
1)Se presentan cartas con ilustraciones que permita observar la cantidad.

2) Luego las cartas tendrán escrito el numeral, de esta manera evitamos que los chicos puedan contar la cantidad presente y que asocien el numerar con la cantidad indicada.

3) Modificación con respecto a la numeración a trabajar.
Para niños de 5 años se pueden emplear cartas del 1 al 10, comenzando la escala a partir del 5.
Objetivo del juego: reconocer el anterior y el siguiente de un número.
Gestión de la clase: no sólo aceptar, preguntar al alumno cómo sabe que es el siguiente. Es esperable que, a partir de 4 y 5 años, reconozca que el que sigue es mayor y el anterior es menor al número dado,
Para alumnos de 1er. grado se trabajará el siguiente es “uno más que” y el anterior es “uno menos que”, que es lo que queremos enseñar.
A partir del juego se podrán trabajar distintas descomposiciones de los números. Ejemplo. 3 + 1 = 2 + 2 etc.
Seguir de a 10.
Material: banda de números
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
Cartas numeradas de 20 al 99.
Cantidad de jugadores: 4 por grupo.
Desarrollo. Se reparten 5 cartas a cada integrante. El primero coloca, si tiene, una carta que sea 10 más que la que corresponde a la banda. Por ejemplo: si 22, la coloca debajo de cada del 12 porque es 10 más que 12. Gana el primeo que se descarta.
Objetivo reconocer el número que es diez más o diez menos que otro.
Gestión de la clase: trabajar con los alumnos la regularidad que se observa. La cifra de las unidades que no cambia y la decena que si.
Juegos de emboque
Salas de 4 y 5 años
Material: canastas (recipientes donde se coloquen pelotitas), pelotitas plásticas.
Cantidad de jugadores: distintos grupos de igual cantidad de alumnos,
Desarrollo: cada niño tira una pelotita tratando de embocarlas en una de las canastas. Gana el grupo que emboca mayor cantidad de pelotitas.
Tema a enseñar: el número como memoria de la cantidad.
Gestión de la clase: para nivel inicial: dejar que los niños indiquen cuántas pelotitas hay en cada canasta y decidan quien ganó.
Observar como cuentan la cantidad de pelotitas. Si señalan cada una a medida que cuentan, si pueden determinar la cantidad sólo mirando, etc.
Jugando con números. 2do.- 3er. Grado.
Material: fichas o tarjetas con números del 1 al 9.
Desarrollo: con las fichas o tarjetas, sin repetirlas, deberán formar distintas sumas que den 15 puntos.
Gestión de la clase: el juego permite ejercitar el cálculo mental. Se continuará analizando las distintas escrituras: 6 + 9 y 9 + 6 trabajando las propiedades conmutativa y asociativa. 1 + 5 + 9 = 5 + 1 + 9
En tercer grado se pueden avanzar analizando cuántas sumas se pueden escribir con dos cartas, (con dos sumandos), con tres y con cuatro.
Armar números – 3er.grado
Material: cartones con números del 0 al 9. Sólo un juego para evitar la repetición de cifras en un mismo número.
Número de jugadores: dos por grupo.
Desarrollo: repartir tres cartones para cada jugador. A una indicación del docente deben formar números de tres cifras. No pueden repetir el número formado. Gana el que forma el mayor. Hacer un registro con los números obtenidos por ambos jugadores.
Por ejemplo cartones 4; 8; 3 y 9; 1, 5
| Jugador 1 | Jugador 2 |
| 483 | **951** |
| **843** | 519 |
| 834 | **915** |
Modificación 1: se puede pedir el menor número es el que gana.
Modificación 2: se pueden formar dos grupos de cartones con número del 0 al 9. Esto da la posibilidad de formar números que tengan cifras repetidas.
Gestión de la clase: se pueden trabajar dos conceptos importantes del número, esto motiva dos clases diferentes.
Opción 1 la posición de cada cifra. Por ejemplo. Por qué son diferentes los números 843 y 834. ¿Qué posición ocupa la cifra 3 en el primer número y en el segundo?
Posibles respuestas de los niños. En el primer número el 3 ocupa la posición de los unos (unidades simples) y en el segundo la de dieces (decena),
Si tenés 43 tenés más que 34.
Opción 2: la cantidad de una unidad determinada. Por ejemplo. Cuántos dieces hay en el número 843.
Juegos para trabajar las operaciones.
Lotería de sumas. Sala de 5 años
Material: Cartones con números desde el 1 hasta el 12, colocados al azar. Dos dados.
Número de jugadores. El grupo completo, pueden trabajar cada uno solo o bien de a dos.
Desarrollo: se tiran ambos dados se suman y se colocan, si está, sobre el número en el cartón.
Lotería: 1er. grado.
Material: Material: Cartones con números desde el 1 hasta el 50, colocados al azar. Dos dados de distinto color. Uno azul que indica la cantidad de dieces (decenas) y otro rojo, que indica la cantidad de unos (unidades simples).
Fichas para ubicar sobre los números.
Número de jugadores. El grupo completo, pueden trabajar cada uno solo o bien de a dos.
Desarrollo: si tira el dado azul, se indica la cantidad de decenas (por ejemplo 4 dieces) y luego el rojo ( 7 unos), Se forma el 47
Aquel que haya colocado bien los números y completado el cartón es el ganador.
Jugando con sumas. 2do. Grado
Material: cartas numeradas del 1 al 10. (Se puede usar la baraja española)
Cantidad de jugadores: grupos de tres chicos.
Desarrollo: se reparten las cartas entre dos jugadores sentados uno frente al otro con el mazo de cartas boca abajo.
Sucesivamente cada jugador toma una carta del montón y la muestra al otro, sin ver la carta propia. El tercer jugador recibe las dos cartas, las mira y anuncia la suma de ambas.
Cada uno de los jugadores tiene que decir cuál fue el número de su carta. El que primero la dice se lleva ambas cartas. Gana el que acumula mayor cantidad de cartas.
Los chicos se van turnando en su función de jugador y secretario.
¿Qué es una situación problemática?.
Son todas aquellas actividades que se preparan para enseñar algún tema: algún concepto del número, las operaciones, las figuras geométricas, etc. Pueden ser presentadas por medio de distintos contextos, cotidianos y sólo numéricos. Con soporte gráfico, con tablas, etc.
Es importante que los niños de sala de 3 años comiencen a resolver problemas en situaciones vivenciales para que, luego en otras salas comiencen a codificar las situaciones.
Veamos un ejemplo:
Jugando con pelotas.
Materiales: pelotas una cada dos niños.
Cantidad de jugadores: dos niños por equipo.
Primer momento: permitir que los niños resuelvan la situación solos. Se los lleva al patio y se indica. Debemos dar una pelota cada dos chicos, ¿cuántas habrá que preparar?
Segundo momento: en la sala, pedirle a los niños que expliquen qué hicieron. Sugerir que esquematicen la situación, el docente presenta una forma de esquema, para que los niños la continúen. (esperable para niños de 4 años)
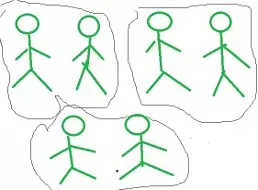
Tercer momento: proponer una situación similar que no pueda ser resuelta con los objetos concretos, de manera de obligar a los alumnos a buscar otros medios.
Al presentar un nuevo juego debe dejarse que los alumnos manipulen el material, lo conozcan, experimenten con él.Luego debe haber una fase o momento de formulación, los alumno se preguntarán ¿qué puede hacerse con este material?. La observación desorganizada hasta ese momento se estructura y comienzan a establecerse las reglas del juego.
Los niños observan el material que se les ha entregado, por ejemplo bolsitas (con mijo) las miran, las arrojan, las sopesan y luego de ubicarlas en algún recipiente (embocar). Es aquí el momento de presentar las reglas del juego a realizar.
Si se trabaja con niños de 4, 5 años, se puede dejar que ellos indiquen las reglas que les parece se pueden emplear. Verificar si sirven, si generan un juego placentero, entretenido, efectivo e ir cambiándolas a medida que van trabajando sobre el material, hasta establecer aquellas que serán las más eficaces.
Jugando con aros. Salas de 3, 4, 5 años.
Material: aros de mimbre.
Número de jugadores: toda la clase. Luego pueden formar grupos de 4 cuatro.(dependiendo de la edad de los chicos).
Desarrollo: darle los aros y dejarlos que los reconozcan. Que los arrojen, entren y salgan de ellos, etc.
Luego se les indicará que los coloquen en el suelo a una distancia determinada (el docente puede colocar una serie de marcas para guiar a los chicos). Explicar las reglas del juego. Por ejemplo. Ir saltando de aro en aro hasta llegar al final de la hilera. Pueden tener colores azul y rojo, colocados en forma alternada. Pedirle que salten de un aro de un color a otro del mismo color, etc.
Las distintas reglas se irán construyendo de acuerdo a lo que los chicos vayan planteando. Lo importante será poder acordar algunas en particular y jugar en consecuencia.
Segundo momento: en la sala, sobre un papel afiche reproducir la hilera formada con los aros y pedirle que expliquen que fue lo que hicieron.
Tercer momento. Numerar la hilera 1, 2, 3, 4 hasta el número que los chicos puedan reconocer (depende de la edad de ellos), jugar con fichas y con un dado.
La geometría es la rama de la Matemática que más se presta a ser enseñada empleando juegos. Emparentada con el arte se presenta más atractiva para que tanto niños como jóvenes aborden su aprendizaje más contentos.
Surgen varios interrogantes:
Juegos de encastre. Salas de 3- 4 años.
Existen muchos juegos de encastre en los cuales los chicos deben hacer pasar un objeto con determinada forma (triangular, rectangular, hexagonal, octogonal, etc). Por una abertura que coincide con ellas.
En general los niños están habituados a estos juegos y no se requieren consignas muy elaboradas para que realicen la tarea, incluso algunos pueden realizarla solo mirando a algún compañero o bien, procediendo por ensayo – error.
En esa edad les gusta poner juntos los que van juntos, es decir aquellos objetos que tienen características comunes, por lo tanto repiten la acción sin dificultad y con gran placer.
Gestión de la clase: el docente puede trabajar el nombre de las piezas con el fin de pedirla si es una de las que falta en el grupo a encastrar. No significa esto que sea un objetivo imperioso de conseguir, pero si de intentar ya que muchos niños memorizan nombres sin dificultad.
Deberá trabajar por medio de preguntas sobre cómo se dan cuenta por donde colocar las piezas, que formas tienen, que diferencian encuentras, etc.
Es importante variar las formas geométricas a emplear no quedarse con las clásicas que se presentan en los jardines y primarios y que parecen ser las únicas existentes, nos referimos a los triángulos, rectángulos y cuadrados, También no insistir en clasificaciones del tipo cuerpos geométricos que ruedan o no ruedan, esto lleva a error y no hace referencia a las caras curvas que es lo que se quiere que observen. (Un cubo arrojado con fuerza “rueda”),
Objetivo del la actividad: familiarizarse con las formas geométricas independientemente de la posición. (Si trabajamos con niños de 3 años).
Identificar formas en objetos y en las aberturas a encastrar. (Si trabajamos con niños de 5 años)
Reconocer características comunes a distintas formas independientes de su posición.( sala de 5 años).
Tangram con piezas de bordes curvilíneos.
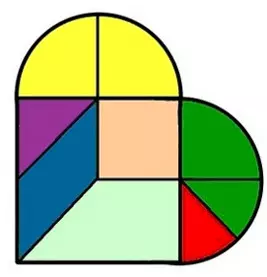
Explorando las figuras. 1er. – 2do. grado
Material: rompecabezas de lados curvos.
Cantidad de jugadores: cuatro por grupo.
Desarrollo: pedir a los niños que formen distintas figuras con las piezas del rompecabezas.
Gestión de la clase: observar que figuras forman, si forman un círculo (hay cuatro figuras que son ¼ de círculo), nombrarlo y hacer notar el lado curvo. Frente a cualquier otra figura que posea un lado curvo preguntar y hacer notar sobre la cantidad de lados rectos y curvos que posea.
Por ejemplo : 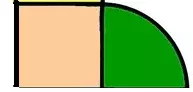
Tres lados rectos y un lado curvo.
1ero. 2do y 3er grado
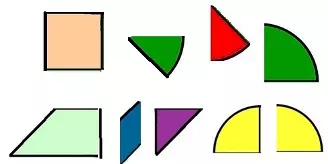
Material: rompecabezas de lados curvos.
Cantidad de jugadores: dos por grupos.
Desarrollo: se reparten las piezas entre ambos jugadores. El primero coloca una pieza en el centro de la mesa y, por turno, van agregando hasta formar la figura original.
En primer grado; primero dejar que tengan el modelo original a la vista.
En segundo y tercer grado, dejar que observen la figura en tiempo determinado y luego quitarla de la vista.
Gana el equipo que termine primero y haya armado bien la figura original.
El docente debe estar abierto a implicarse dentro del juego.
Previo al juego, con la elección, selección, planificación. Con la previsión de tiempos y espacios y, con la selección de los materiales.
Durante el juego, tomar el lugar de observador para saber qué es lo que está sucediendo, qué es lo que hace falta e intervenir, si es necesario, para potenciar y enriquecer la situación de juego y generar mayores aprendizajes. También, para ofrecer otras oportunidades para lograr nuevos descubrimientos en los modos de jugar.
Al finalizar el juego, haciendo una revisión de los momentos más significativos para fijar los contenidos trabajados. Es conveniente que realice un registro del trabajo de los alumnos para tener la posibilidad de volver sobre él y planificar futuras actividades
Los juegos permiten:
A los docentes les permite acercar más fácilmente las dificultades y necesidades de sus alumnos, porque crea un ambiente ameno lo que les permite expresarse mejor. También le sirve como un momento de evaluación sn la presión de las evaluaciones tradicionales
A los alumnos: el juego es una situación real de comunicación en la cual los alumnos ponen en práctica sus habilidades comunicativas ya que para poder participar activamente del juego, el alumno necesita argumentar, expresar sus sentimientos e ideas y defender su punto de vista, practicando y desarrollando procesos mentales y emocionales que se van a activar siempre que se someta a una situación de comunicación.
Muchos chicos “sufren” la adquisición de conceptos matemáticos, sin embargo disfrutan con juegos y puzzles Permite el desarrollo de aspectos cognitivos y de actitudes sociales como la iniciativa, la responsabilidad, el respeto, la creatividad, entre otros.
Los motiva y disminuye la ansiedad en la medida en que, en esas actividades, es posible reducir la importancia de los errores y entenderlos como parte del proceso de aprendizaje. Les permite tomar más confianza en sus acciones y se sienten libres para participar. Emplear juegos en la enseñanza puede llevarlos a que no sientan que su paso por la matemática es un fracaso
Kaczmarzyk , P.Lic , Prof. Lucena, M. Juego en el Nivel Inicial. Dirección General de cultura y Educación. Gobierno de la Pcia. de Bs.As. Circular Nº 5 2007 https://servicios2.abc.gov.ar/lainstitucion/sistemaeducativo/educacioninicial/capacitacion/documentoscirculares/2007/circular5.pdf(https://servicios2.abc.gov.ar/lainstitucion/sistemaeducativo/educacioninicial/capacitacion/documentoscirculares/2007/circular5.pdf)
Diseño curricular para la Escuela Primaria. Educación General Básica. 1er. Ciclo Gobierno de la Ciudad de Bs. As. Secretaria de Educación . Diseño de Currícula. 2004. Buenos Aires.
Diseño curricular para el Nivel Inicial Gobierno de la Ciudad de Bs. As. Secretaria de Educación . Diseño de Currícula. 2001. Buenos Aires.
Berdichevsky, P, Saguier, A, Castro, A Números en juego. Zona fantástica
de Guzmán, M/.Juegos matemáticos en la enseñanza. Facultad de Matemáticas Universidad Complutense de Madrid
Cerquetti Aberkane, F; Berdonneau,K; Enseñar Matemática en el Nivel Inicial. 1994. Editorial Hachette. Buenos Aires.
Saiz, I, Parra, C. Hacer Matemática en 2do.. Ed. Estrada.2.010
Saiz, I, Parra, C. Hacer Matemática en 3ero. Ed. Estrada.2.010
Villabrille , B El juego en la enseñanza de las matemáticas Instituto Superior Pedro Poveda Buenos Aires (Argentina)
Cuadernos para el aula 1ero y 3ero. Dirección Nacional de Gestión Curricular y Formación Docente Bs.As. 2006
 Ecuaciones :primera parte Participación e interés: ausentes en la clase de matemática. Secuencia de actividades para medir ángulos La probabilidad y la escuela primaria El Lenguaje y la Matemática La enseñanza de la divisibilidad. ¿Proporcionalidad o regla de tres?. Capacitación Docente EL cálculo Mental o el cálculo Pensado
Ecuaciones :primera parte Participación e interés: ausentes en la clase de matemática. Secuencia de actividades para medir ángulos La probabilidad y la escuela primaria El Lenguaje y la Matemática La enseñanza de la divisibilidad. ¿Proporcionalidad o regla de tres?. Capacitación Docente EL cálculo Mental o el cálculo Pensado